2018年普通高等學(xué)校招生全國統(tǒng)一考試數(shù) 學(xué)（理）（北京卷）

第一部分（選擇題共40分）

一、選擇題共8小題，每小題5分，共40分。在每小題列出的四個選項中，選出符合題目要求的一項。

（1）已知集合A={x||x|<2}，B={–2，0，1，2}，則AB=

（A）{0，1}（B）{–1，0，1}

（C）{–2，0，1，2}（D）{–1，0，1，2}

（2）在復(fù)平面內(nèi)，復(fù)數(shù)的共軛復(fù)數(shù)對應(yīng)的點位于

（A）第一象限（B）第二象限

（C）第三象限（D）第四象限

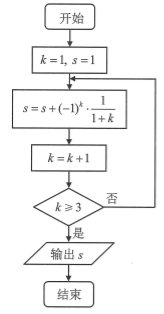
（3）執(zhí)行如圖所示的程序框圖，輸出的s值為

（A）（B）

（C）（D）

（4）“十二平均律”是通用的音律體系，明代朱載堉最早用數(shù)學(xué)方法計算出半音比例，為這個理論的發(fā)展做出了重要貢獻(xiàn)．十二平均律將一個純八度音程分成十二份，依次得到十三個單音，從第二個單音起，每一個單音的頻率與它的前一個單音的頻率的比都等于．若第一個單音的頻率為f，則第八個單音的頻率為

（A）（B）

（C）（D）

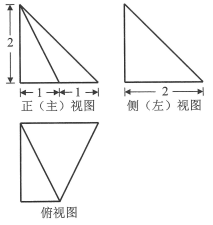
（5）某四棱錐的三視圖如圖所示，在此四棱錐的側(cè)面中，直角三角形的個數(shù)為

（A）1（B）2

（C）3（D）4

（6）設(shè)a，b均為單位向量，則“”是“a⊥b”的

（A）充分而不必要條件（B）必要而不充分條件

（C）充分必要條件（D）既不充分也不必要條件

（7）在平面直角坐標(biāo)系中，記d為點P（cosθ，sinθ）到直線的距離，當(dāng)θ，m變化時，d的最大值為

（A）1（B）2

（C）3（D）4

（8）設(shè)集合則

（A）對任意實數(shù)a，（B）對任意實數(shù)a，（2，1）

（C）當(dāng)且僅當(dāng)a<0時，（2，1）（D）當(dāng)且僅當(dāng)時，（2，1）

第二部分（非選擇題共110分）

二、填空題共6小題，每小題5分，共30分。

（9）設(shè)是等差數(shù)列，且a1=3，a2+a5=36，則的通項公式為__________．

（10）在極坐標(biāo)系中，直線與圓相切，則a=__________．

（11）設(shè)函數(shù)f（x）=，若對任意的實數(shù)x都成立，則ω的最小值為__________．

（12）若x，y滿足x+1≤y≤2x，則2y?x的最小值是__________．

（13）能說明“若f（x）>f（0）對任意的x∈（0，2］都成立，則f（x）在［0，2］上是增函數(shù)”為假命題的一個函數(shù)是__________．

（14）已知橢圓，雙曲線．若雙曲線N的兩條漸近線與橢圓M的四個交點及橢圓M的兩個焦點恰為一個正六邊形的頂點，則橢圓M的離心率為__________；雙曲線N的離心率為__________．

三、解答題共6小題，共80分。解答應(yīng)寫出文字說明，演算步驟或證明過程。

（15）（本小題13分）

在△ABC中，a=7，b=8，cosB=–．
（Ⅰ）求∠A；

（Ⅱ）求AC邊上的高．

（16）（本小題14分）

如圖，在三棱柱ABC?中，平面ABC，D，E，F，G分別為，AC，，的中點，AB=BC=，AC==2．

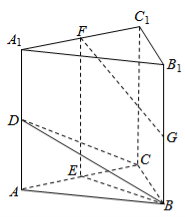
（Ⅰ）求證：AC⊥平面BEF；

（Ⅱ）求二面角B?CD?C1的余弦值；

（Ⅲ）證明：直線FG與平面BCD相交．

（17）（本小題12分）

電影公司隨機收集了電影的有關(guān)數(shù)據(jù)，經(jīng)分類整理得到下表：

好評率是指：一類電影中獲得好評的部數(shù)與該類電影的部數(shù)的比值．

假設(shè)所有電影是否獲得好評相互獨立．

（Ⅰ）從電影公司收集的電影中隨機選取1部，求這部電影是獲得好評的第四類電影的概率；
（Ⅱ）從第四類電影和第五類電影中各隨機選取1部，估計恰有1部獲得好評的概率；
（Ⅲ）假設(shè)每類電影得到人們喜歡的概率與表格中該類電影的好評率相等，用“”表示第k類電影得到人們喜歡，“”表示第k類電影沒有得到人們喜歡（k=1，2，3，4，5，6）．寫出方差，，，，，的大小關(guān)系．

（18）（本小題13分）

設(shè)函數(shù)=[]．

（Ⅰ）若曲線y= f（x）在點（1，）處的切線與軸平行，求a；

（Ⅱ）若在x=2處取得極小值，求a的取值范圍．

（19）（本小題14分）

已知拋物線C：=2px經(jīng)過點（1，2）．過點Q（0，1）的直線l與拋物線C有兩個不同的交點A，B，且直線PA交y軸于M，直線PB交y軸于N．

（Ⅰ）求直線l的斜率的取值范圍；

（Ⅱ）設(shè)O為原點，，，求證：為定值．

（20）（本小題14分）

設(shè)n為正整數(shù)，集合A=．對于集合A中的任意元素和，記

M（）=．

（Ⅰ）當(dāng)n=3時，若，，求M（）和M（）的值；

（Ⅱ）當(dāng)n=4時，設(shè)B是A的子集，且滿足：對于B中的任意元素，當(dāng)相同時，M（）是奇數(shù)；當(dāng)不同時，M（）是偶數(shù)．求集合B中元素個數(shù)的最大值；

（Ⅲ）給定不小于2的n，設(shè)B是A的子集，且滿足：對于B中的任意兩個不同的元素，

M（）=0．寫出一個集合B，使其元素個數(shù)最多，并說明理由．